Differentiation - what is it?

Okay so in Maths we learn about differentiation and what to do, the formulas etc, but what is differentiation???

Differentiation is finding the slope of a curve at a particular point on the curve.

Eg:

But how do we find slopes?

First consider a straight line:

We get the slope of a straight line by taking two points on the line and using their co-ordinates (x1, y1) and (x2, y2) in a slope formula:

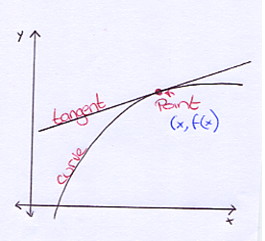
From functions, we know that a point x has a height of f(x), (i.e. y = f(x) ) :

 

 Something else to consider is that the slope at a point on a curve is the same slope as the tangent at that point

 

So if we know two points on the tangent we can work out the tangent slope and thus the curve slope.


Next we require some limits and some imagination.


Picture our curve and tangent:

 

 

Now zoom in on our point:

And again:

And again... It's getting hard to distinguish between the two lines.

We can soom in infintely until they appear as practically the same line! so we can now say that two points on the curve are now alone on the tangent, a distance of  'h' apart.

The second point becomes (x+h, f(x+h) )

If we make the distance 'h' between the two points as small as possible t will appear as if they are the same point.

Beacause we have two points we can use our slope formula

  

Using our co-ordinates (x, f(x) ) and (x+h, f(x+h) ) this formula becomes:

f(x+h) - f(x) 

(x+h) - x

Subtracting the 'x' on the bottom lines makes this:

f(x+h) - f(x) 

h

Now we wat to make the 'h' as small as possible so we limit h - 0

  Slope = lim  f(x+h) - f(x) 

       h-0           h

This is our differentiation formula!

We can apply this to any curve:

Example: